The Reynolds number is undoubtedly the most famous dimensionless
parameter in fluid mechanics. It is named in honor of Osborne Reynolds (1842–1912), a




British engineer who first demonstrated that this combination of variables could be used as a criterion
to distinguish between laminar and turbulent flow. In most fluid flow problems there will
be a characteristic length, and a velocity, V, as well as the fluid properties of density, and
viscosity, which are relevant variables in the problem. Thus, with these variables the Reynolds
number

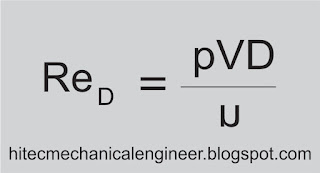Reynolds Number

arises naturally from the dimensional analysis. The Reynolds number is a measure of the ratio of
the inertia force on an element of fluid to the viscous force on an element. When these two types
of forces are important in a given problem, the Reynolds number will play an important role. However,
if the Reynolds number is very small xthis is an indication that the viscous forces
are dominant in the problem, and it may be possible to neglect the inertial effects; that is, the density
of the fluid will not be an important variable. Flows at very small Reynolds numbers are commonly
referred to as “creeping flows”. Conversely, for large Reynolds
number flows, viscous effects are small relative to inertial effects and for these cases it may be
possible to neglect the effect of viscosity and consider the problem as one involving a “nonviscous”
fluid. This type of problem is considered in detail in Sections 6.4 through 6.7. An example
of the importance of the Reynolds number in determining the flow physics is shown in the figure
in the margin for flow past a circular cylinder at two different Re values